MMath project for 2020-21

The ability to create visualisations of mathematical surfaces or diagrams is an immensely important skill that has been rarely addressed in your studies at Bath. This is a project about the visualisation of maths.

With the advent of desktop computers and home publishing software, many of us have moved away from meticulously hand-drawn technical illustrations and rely on electronic generation of figures using software like Matlab or Mathematics. However, there are many advantages to traditional visualisations. Compare the clarity and usefulness of these two representations of the Gamma function. The first one that you see is generated from Mathematica.

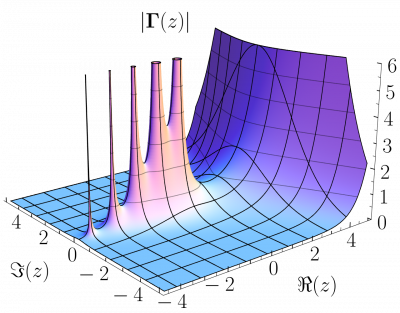
The second one is a hand-drawn picture from Jahnke and Emde over a century older and from 1909! Notice how the hand-drawn picture allows for the emphasis of certain features that are absent from the electronically generated one.

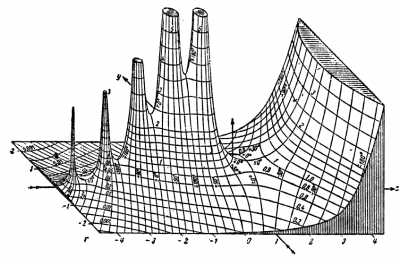
How do we design computational algorithms for converting from a given electronic representation of a surface to what looks like a hand-drawn sketch. This is one of the key questions in a very active field known as Non-Photorealistic Rendering (NPR). Although such methods are well-known to industry experts (and are sometimes found on commercial software), they are often not appropriate for use by scientists and mathematicians.

Another interesting question is how to render the output of high-dimensional flow data (such as from a fluid dynamics simulation) in a way that is visually appealing and informative. This is quite a complicated question, but it quickly becomes clear that traditional methods of plotting will often fail.

In this project, the student will develop (home-grown) techniques for non-photorealistic rendering (NPR) and apply them to produce visualisations of mathematical surfaces and fields. This involves learning about NPR techniques, as well as general techniques of computer graphics (e.g. ray theory). The project will involve a very nice mixture of mathematics and numerical algorithms with programming. The project can move from quite theoretical questions (efficiency and design of algorithms) to practical implementation.

The main type of surfaces that you might seek to illustrate are so-called Riemann surfaces. For example, here is a picture of a Riemann surface that comes up in my research on hydrodynamics and water waves. During the project, you will learn more about these surfaces.

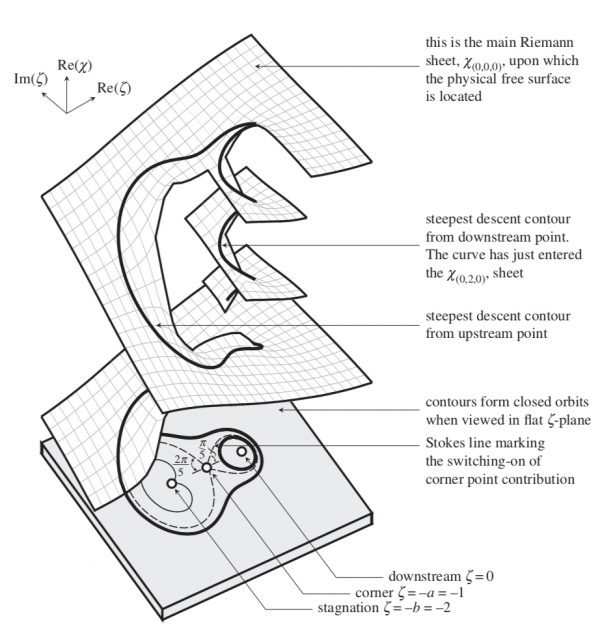
If you are interested in finding out more about the mathematics and computation, you can Google “non-photorealistic rendering” and perhaps have a look at

1. Strothotte & Schlechtweg (2002) Non-photorealistic Computer Graphics Modeling, Rendering, and Animation. San Francisco, CA: Morgan Kaufmann. (Copy available in Bath library).
2. Praun et al. (2001) Real-time hatching.
3. Francis (2002) A topological picturebook. Springer.
   1. A book that is all about drawing surfaces in mathematics.

Desireables:

1. A student who enjoys visualisation, art, and technical drawing
2. An aptitude for coding. We will begin with Matlab or Python, but you may need to learn with a 'heavier' object-oriented language like C/C++.
3. An interest in numerical algorithms and computer graphics
4. Good abilities in vector calculus (MA20223) and geometry. There will be some elements of complex analysis (as they provide examples of interesting surfaces).

Prerequisites: No strict pre-requisites, but students who took CM30075 (Advanced Computer Graphics) should definitely inquire.

I'm using this space to add further references when I encounter them. They may give you a better idea of the mathematics involved.

1. A topological picturebook by George Francis: an actual book about how to sketch topological surfaces written by a mathematician.
2. Visual Complex Analysis: Tristan Needham's famous book which gave a visual twist to complex variables. Apparently he has been working on a new book on differential geometry that is set to be published later this year.
3. A discussion on MathOverflow about books similar to Needham's. It is worth looking at David Hilbert's 1952 book referenced in that discussion for many beautiful images.
4. Nonphotorealistic rendering in scientific visualisation: a lot of interesting articles in this compilation from SIGGRAPH 2001.
5. Victoria Interrante has many interesting articles on her website and works at the intersection of science and visualisation. Might be worth having a quick look at some of the preliminary chapters of her 1996 thesis. Perhaps find a copy of her article Art and Science in Visualization
6. NYU PhD 2001 thesis by Aaron Hertzmann on Algorithms for rendering in artistic styles; the Chapter 5 notes inspiration from A Topological Picturebook and is of interest.
7. Work by Scalera et al.: looks to be a simple cross-hatching algorithm applied to rasterised images.
8. Rendering parametric surfaces in pen and ink: 1996 paper; this looks really excellent starting point. They discuss the differential geometry required.
9. Another paper that was part of the Refs [33-35] from the Italian work by Scalera et al. above. Another good reference.